Математички задачи кои учениците од Сингапур ги добиваат на тестовите. Дали вие можете да ги решите?
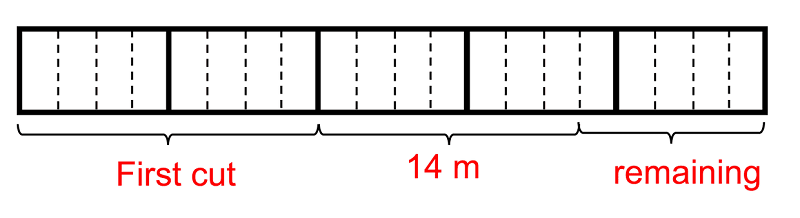
1. Мери исече 2/5 од парче конец. Подоцна, таа исече уште 14 метри. Соодносот на должината на конецот кој остана со вкупната исечена должина е 1:3. Која е должината на останатиот конец?
А. 5 метри
B. 7 метри
C. 10 метри
D. 14 метри
2. Областите на лицето на правоаголна кутија се 84 cm2, 70 cm2 и 30 cm2. Koj e волуменот на кутијата?
A. 300 cm3
B. 420 cm3
C. 490 cm3
D. 504 cm3
3. Постојат четири броеви. Ако изоставиме еден број, просекот на останатите три броеви ќе биде 45, 60, 65 и 70. Кој е просекот на останатите четири броеви?
A. 50
B. 55
C. 60
D. 65
4. Еден марш од низ улиците, од училиштето (S) до Центарот за заедница (СС). Една од улиците е затворена. Ако маршот може да патува само од исток кон југ, кој е бројот на различни можни начини на кој може да стигне до Центарот за заедница?
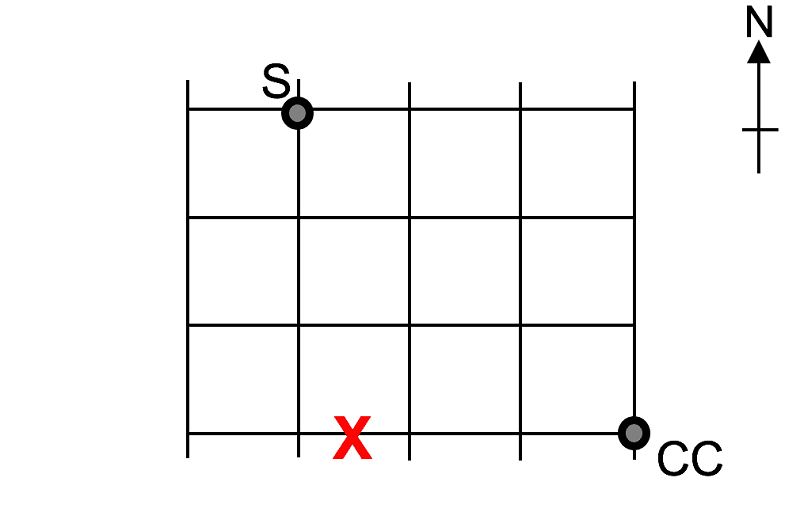
A. 16
B. 19
C. 20
D. 22
5. На Сали ѝ бил даден 5 сет карти нумерирани од 1 до 5. Истото било направено и со Питер. Потоа и на двајцата им биле врзани очите - со така врзани очи тие извлекле карта од нивните сетови. Сумата на броевите од двете картички ѝ бил кажан само на Сали, а производот на броевите му бил кажан само на Питер. Потоа и двајцата требало да ги погодат броевите. Подолу е што тие двата кажале:
Питер: Не ги знам двата броеви.
Сали: Сега јас ги знам двата броеви.
Питер: Јас се'уште не ги знам двата броеви.
Сели: Јас ќе ти помогнам. Бројот кој ми го кажаа беше поголем од бројот што ти го кажаа тебе.
Питер: Сега јас ги знам двата броеви.
Кои се двата броеви?
А. 1 и 4
B. 1 и 5
C. 2 и 4
D. 2 и 5
6. Има 4 клучеви и 4 брави. Кој е максималниот број на пати за да ги пробате клучевите за конечно да ги пронајдете паровите на клучеви и брави?
A. 4
B. 6
C. 10
D. 16
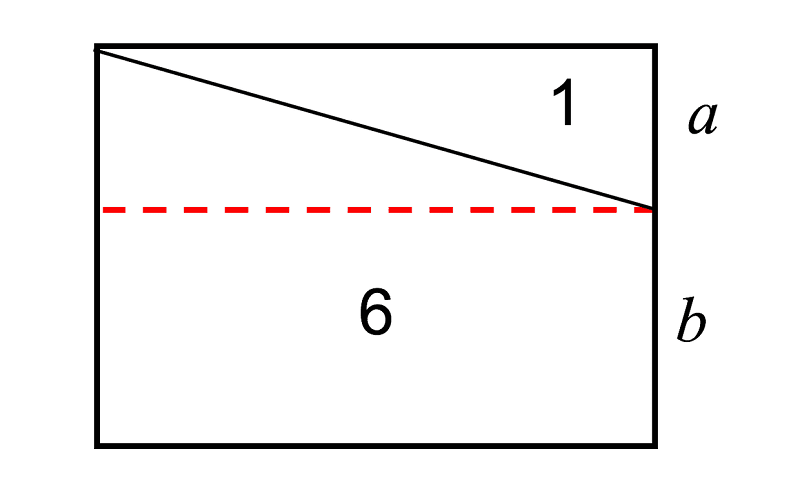
7. Во дијаграмот, наведената линија ја дели областа на правоаголникот во сооднос 1:6. Кој е соодносот а:b?
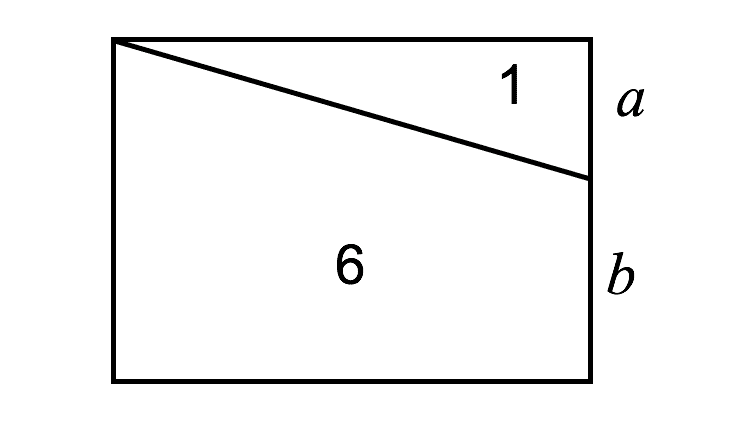
A. 2 : 3
B. 1 : 2
C. 2 : 5
D. 1 : 3
8. Колку пати стрелката за часот и стрелката за минути од еден часовник формираат прав агол еден со друг помеѓу 0600 и 1200 истиот ден?
A. 11
B. 12
C. 23
D. 24
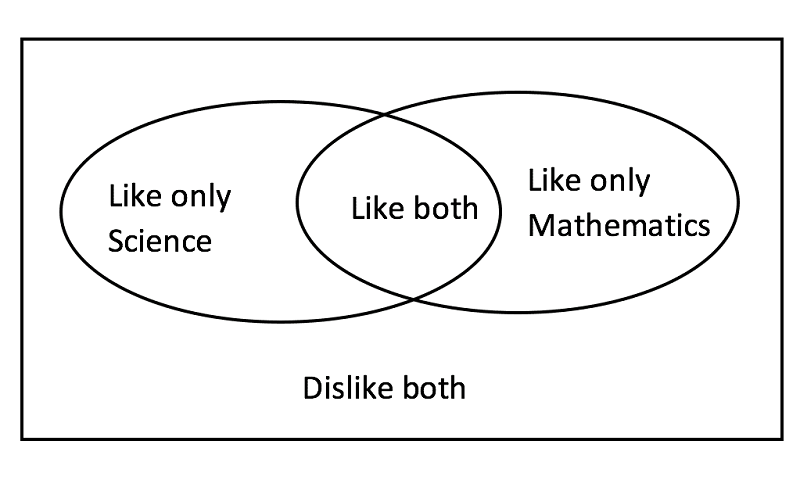
9. Има 240 ученици во шесто одделение. Соодносот на бројот на ученици кои сакаат наука со бројот кои не сакаат е 5:3. Соодносот на бројот на ученици кои сакаат математика со оние кои не сакаат е 7:5. Бројот на ученици кои сакаат и математика и наука е 86. Колку ученици не сакаат наука и математика?
А. 32
B. 36
C. 40
D. 48
10. Мојот наставник имаше 3 големи кутии благи. Секоја кутија содржеше благи со различни бои. На секој ученик му беа дадени 5 благи со две различни бои. Ако секој ученик во класот би добил различна комбинација на бои, кој беше најголемиот можен број на ученици во класот?
A. 8
B. 12
C. 16
D. 64
Одговори:
1. Решението е под С
2. Решението е под В.
3. Решението е под C.
4. Решението е под В.
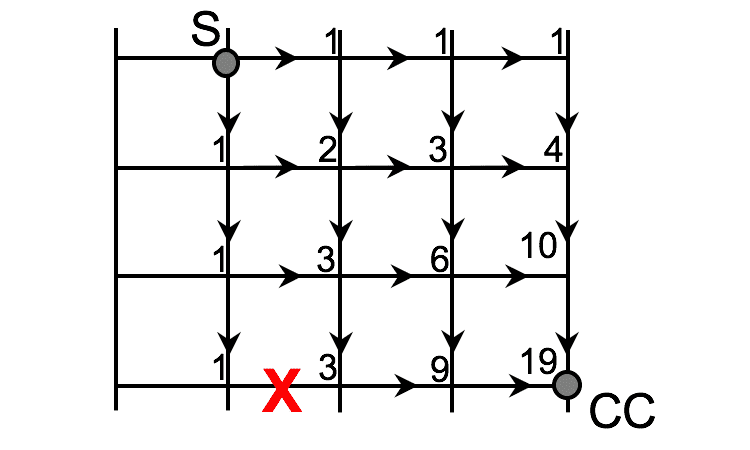
5. Решението е под А.
6. Решението е под В.
7. Решението е под С.
8. Решението е под А.
9. Решението е под В.
10. Решението е под В.